Soal Vektor dan Peluang
1.VEKTOR
Pengertian vektor

Pada garis berarah dari titik A ke titik B di R 3 mempunyai panjang tertentu dinyatakan sebagai vektor. Vektor dapat dinotasikan dengan :

Atau dapat juga dinyatakan sebagai :

Dimana adalah vektor satuan.
adalah vektor satuan.
Jika titik A (x1,y1,z1) dan B (x2,y2,z2) maka vektor AB adalah :




 maka vektor satuan dari a adalah:
maka vektor satuan dari a adalah:

a. Penjumlahan atau pengurangan vektor

Contoh :
Diketahui vektor Nilai
Nilai 
Jawab :


b. Perkalian Skalar dengan vektor

a. Perkalian Skalar

b. Cross Product








d. Rumus Pembagian


Contoh :
Diketahui titik A (-4, 1, 3 ), B (6, -4, 3) dan C (4, 5, -1) Titik R membagi AB sehingga 2AR = 3RB, vektor yang mewakili adalah :
adalah :
Jawab :
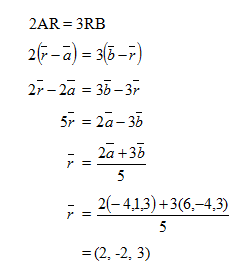

Soal vektor
Pengertian vektor

Pada garis berarah dari titik A ke titik B di R 3 mempunyai panjang tertentu dinyatakan sebagai vektor. Vektor dapat dinotasikan dengan :

Atau dapat juga dinyatakan sebagai :

Dimana
 adalah vektor satuan.
adalah vektor satuan. - Panjang Vektor
Jika titik A (x1,y1,z1) dan B (x2,y2,z2) maka vektor AB adalah :




- Vektor Satuan
 maka vektor satuan dari a adalah:
maka vektor satuan dari a adalah: 
- Operasi Penjumlahan, Pengurangan dan Perkalian Vektor dangan Skalar
a. Penjumlahan atau pengurangan vektor

Contoh :
Diketahui vektor
 Nilai
Nilai 
Jawab :


b. Perkalian Skalar dengan vektor

- Rumus Perbandingan, Perkalian Skalar Proyeksi dan Perkalian Silang Vektor
a. Perkalian Skalar

b. Cross Product








d. Rumus Pembagian


Contoh :
Diketahui titik A (-4, 1, 3 ), B (6, -4, 3) dan C (4, 5, -1) Titik R membagi AB sehingga 2AR = 3RB, vektor yang mewakili
 adalah :
adalah : Jawab :
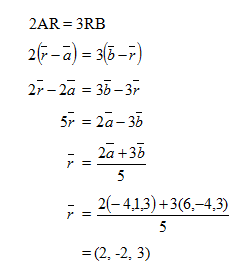

Soal vektor
- Dua buah vektor A dan B mengapit sudut 120o. Resultan kedua vektor adalah 20√3 N. Jika resultan tersebut membentuk sudut 30o terhadap vektor A, maka besar A dan B adalah .....
A. 20 N dan 40 N D. 40√3 N dan 20√3 N B. 40 N dan 20 N E. 20√3 N dan 20√3 N C. 20√3 N dan 40√3 N
Pembahasan :
Jika digambarkan akan terlihat seperti di gambar di bawah ini :
Berdasarkan aturan sinus, maka berlaku :
A = B = R sin 90 sin 30 sin 120 A = R sin 90 sin 120
⇒ A = 40√2 (½√2)A = 20√3 1 (-½)
Besar vektor B dapat dihitung dengan persamaan :
A = R sin 90 sin 120
⇒ A = 40√2 (½√2)A = 20√3 1 (-½)
⇒ T2 = 500 N
Jadi, T1 = T2 = 500 N.
Jawaban : C - Sebuah perahu menyeberangi sungai yang lebarnya 100 m dengan kelajuan 4 m/s tegak lurus terhadap arah arus sungai. Jika air sungai mengalir dengan kecepatan 3 m/s, maka jarak tempuh perahu tersebut sampai di seberang sungai adalah .....
A. 100 m D. 115 m B. 105 m E. 125 m C. 110 m
Pembahasan :
Dik : Vair = Va = 3m/s, Vperahu = Vp = 4 m/s, x = 100 m.
Karena perahu bergerak tegak lurus arah aliran sungai, maka sudut antara Va dan Vp adalah 90o. Dengan begitu kecepatan resultannya dapat dihitung dengan menggunakan dalil Phytagoras sebagai berikut :
⇒ Vr = √Va2 + Vp2
⇒ Vr = √32 + 42
⇒ Vr = 5 m/s.
Sudut yang dibentuk resultan dengan vektor kecepatan air adalah :
⇒ sin a = Vp Vr
⇒ a = 53o.⇒ sin a = 4 5
Dengan demikian, jarak yang ditempuh oleh perahu (s) adalah :
⇒ sin 53o = x s
⇒ s = 125 m.⇒ 4 = 100 5 s
Jawaban : E. - Dua buah vektor gaya P dan R mengapit sudut 53o dan menghasilkan resultan sebesar 40√2 N. Jika P : R = 1 : 5, maka besar vektor P dan Q adalah .....
A. 6 N dan 6 N D. 8 N dan 4 N B. 2 N dan 10 N E. 4 N dan 8 N C. 10 N dan 2 N
Pembahasan :
Dik : R = 15 N, P/R = 1/5, maka R = 5P
Berdasarkan aturan cosinus :
⇒ R = √P2 + R2 + 2PR cos θ
⇒ R = √P2 + (5P)2 + 2P(5P) cos 53o
⇒ R = √P2 + 25P2 + 10P2 (⅗)
⇒ R = √32P2
⇒ R = √(16 x 2)P2
⇒ 40√2 = 4P√2⇒ P = 10NDengan demikian, besar vektor Q adalah :⇒ Q = ⅕ P⇒ Q = ⅕ (10)
⇒ Q = 2 NJawaban : C - Dua buah vektor saling membentuk sudut 67o. Jika resultan membentuk sudut 37o terhadap vektor kedua yang besarnya 15 N, maka besar vektor pertama adalah .....
A. 18 N D. 24 N B. 20 N E. 30 N C. 22 N
Pembahasan :
Dik : F2 = 15 N.
Berdasarkan aturan sinus :
F2 = F1 = R sin 30o sin 37o sin 67o 15 = F1 sin 30o sin 37o
F1 =18 N15 = F1 ½ ⅗
Jawaban : A - Tiga buah vektor A, B, dan C yang setitik tangkap masing-masing besarnya 15 N. Vektor B berada di antara A dan C. Jika sudut antara A dan B sama dengan sudut antara B dan C yaitu 60o, maka resultan ketiga vektor tersebut adalah ....
A. 10 D. 40 B. 20 E. 50 C. 30
Pembahasan :
Diketahui : A = B = C = 15 N.
Dari gambar di atas jelas terlihat bahwa A + C = B. Dengan demikian resultannya adalah :
⇒ R = A + B + C
⇒ R = B + B
⇒ R = 2B
⇒ R = 2(15)
⇒ R = 30 N.
Jawaban di atas juga dapat dibuktikan dengan aturan cosinus. Sudut yang dibentuk oleh A dan C adalah 120o, sehingga :
⇒ A + C = √A2 + C2 + 2A.C cos θ
⇒ A + C = √A2 + A2 + 2A.A cos 120o
⇒ A + C = √2A2 + 2A2 (-½)
⇒ A + C = A
Karena A = B = C = 15 N, maka :
⇒ R = A + B + C
⇒ R = A + C + B
⇒ R = A + B
⇒ R = 15 N + 15 N
⇒ R = 30 N.
Jawaban : C
2.PELUANG
1) Permutasi
Permutasi adalah susunan unsur-unsur yang berbeda dalam urutan tertentu. Pada permutasi urutan diperhatikan sehingga
Permutasi k unsur dari n unsur adalah
semua urutan yang berbeda yang mungkin dari k unsur yang diambil dari n
unsur yang berbeda. Banyak permutasi k unsur dari n unsur ditulis
adalah
semua urutan yang berbeda yang mungkin dari k unsur yang diambil dari n
unsur yang berbeda. Banyak permutasi k unsur dari n unsur ditulis  atau
atau  .
.
Permutasi siklis (melingkar) dari n unsur adalah (n-1) !
Cara cepat mengerjakan soal permutasi
dengan penulisan nPk, hitung 10P4
Contoh permutasi siklis :
kita langsung tulis 4 angka dari 10 mundur, yaitu 10.9.8.7
jadi 10P4 = 10x9x8x7 berapa itu? hitung sendiri
Suatu keluarga yang terdiri atas 6 orang duduk mengelilingi sebuah meja makan yang berbentuk lingkaran. Berapa banyak cara agar mereka dapat duduk mengelilingi meja makan dengan cara yang berbeda?
Jawab :
Banyaknya cara agar 6 orang dapat duduk mengelilingi meja makan dengan urutan yang berbeda sama dengan banyak permutasi siklis (melingkar) 6 unsur yaitu :
2) Kombinasi
Kombinasi adalah susunan unsur-unsur dengan tidak memperhatikan urutannya. Pada kombinasi AB = BA. Dari suatu himpunan dengan n unsur dapat disusun himpunan bagiannya dengan untuk Setiap himpunan bagian dengan k unsur dari himpunan dengan unsur n disebut kombinasi k unsur dari n yang dilambangkan dengan ,
Setiap himpunan bagian dengan k unsur dari himpunan dengan unsur n disebut kombinasi k unsur dari n yang dilambangkan dengan , 
Contoh :
Diketahui himpunan .
.
Tentukan banyak himpunan bagian dari himpunan A yang memiliki 2 unsur!
Jawab :

Banyak himpunan bagian dari A yang memiliki 2 unsur adalah C (6, 2).

Cara cepat mengerjakan soal kombinasi
dengan penulisan nCk, hitung 10C4
kita langsung tulis 4 angka dari 10 mundur lalu dibagi 4!, yaitu 10.9.8.7 dibagi 4.3.2.1
jadi 10C4 = 10x9x8x7 / 4x3x2x1 berapa itu? hitung sendiri
Ohya jika ditanya 10C6 maka sama dengan 10C4, ingat 10C6=10C4. contoh lainnya
20C5=20C15
3C2=3C1
100C97=100C3
melihat polanya? hehe semoga bermanfaat!
Peluang Matematika1. Pengertian Ruang Sampel dan Kejadian
Himpunan S dari semua kejadian atau peristiwa yang mungkin mucul dari suatu percobaan disebut ruang sampel. Kejadian khusus atau suatu unsur dari S disebut titik sampel atau sampel. Suatu kejadian A adalah suatu himpunan bagian dari ruang sampel S.
Contoh:
2. Pengertian Peluang Suatu Kejadian
Diberikan percobaan pelemparan 3 mata uang logam sekaligus 1 kali, yang masing-masing memiliki sisi angka ( A ) dan gambar ( G ). Jika P adalah kejadian muncul dua angka, tentukan S, P (kejadian)!
Jawab :
S = { AAA, AAG, AGA, GAA, GAG, AGG, GGA, GGG}
P = {AAG, AGA, GAA}
Pada suatu percobaan terdapat n hasil yang mungkin dan masing-masing berkesempatan sama untuk muncul. Jika dari hasil percobaan ini terdapat k hasil yang merupakan kejadian A, maka peluang kejadian A ditulis P ( A ) ditentukan dengan rumus :
Contoh :
Pada percobaan pelemparan sebuah dadu, tentukanlah peluang percobaan kejadian muncul bilangan genap!
Jawab : S = { 1, 2, 3, 4, 5, 6} maka n ( S ) = 6
Misalkan A adalah kejadian muncul bilangan genap, maka:
A = {2, 4, 6} dan n ( A ) = 3
3. Kisaran Nilai Peluang Matematika
Misalkan A adalah sebarang kejadian pada ruang sampel S dengan n ( S ) = n, n ( A ) = k dan
Jadi, peluang suatu kejadian terletak pada interval tertutup [0,1]. Suatu kejadian yang peluangnya nol dinamakan kejadian mustahil dan kejadian yang peluangnya 1 dinamakan kejadian pasti.
4. Frekuensi Harapan Suatu Kejadian
Jika A adalah suatu kejadian pada frekuensi ruang sampel S dengan peluang P ( A ), maka frekuensi harapan kejadian A dari n kali percobaan adalah n x P( A ).
Contoh :
Frekuensi harapan munculnya mata dadu 1 adalah
Bila sebuah dadu dilempar 720 kali, berapakah frekuensi harapan dari munculnya mata dadu 1? Jawab :
Pada pelemparan dadu 1 kali, S = { 1, 2, 3, 4, 5, 6 } maka n (S) = 6.
Misalkan A adalah kejadian munculnya mata dadu 1, maka:
A = { 1 } dan n ( A ) sehingga :
5. Peluang Komplemen Suatu Kejadian
Misalkan S adalah ruang sampel dengan n ( S ) = n, A adalah kejadian pada ruang sampel S, dengan n ( A ) = k dan Ac adalah komplemen kejadian A, maka nilai n (Ac) = n – k, sehingga :

Jadi, jika peluang hasil dari suatu percobaan adalah P, maka peluang hasil itu tidak terjadi adalah (1 – P).
Peluang Kejadian Majemuk1. Gabungan Dua Kejadian
Untuk setiap kejadian A dan B berlaku :
Catatan : dibaca “ Kejadian A atau B dan
dibaca “ Kejadian A atau B dan  dibaca “Kejadian A dan B”
dibaca “Kejadian A dan B”
Contoh :
Pada pelemparan sebuah dadu, A adalah kejadian munculnya bilangan komposit dan B adalah kejadian muncul bilangan genap. Carilah peluang kejadian A atau B!
Jawab :
2. Kejadian-kejadian Saling Lepas
Untuk setiap kejadian berlaku Jika
Jika  . Sehingga
. Sehingga  Dalam kasus ini, A dan B disebut dua kejadian saling lepas.
Dalam kasus ini, A dan B disebut dua kejadian saling lepas.
3. Kejadian Bersyarat
Jika P (B) adalah peluang kejadian B, maka P (A|B) didefinisikan sebagai peluang kejadian A dengan syarat B telah terjadi. Jika adalah peluang terjadinya A dan B, maka
adalah peluang terjadinya A dan B, maka  Dalam kasus ini, dua kejadian tersebut tidak saling bebas.
Dalam kasus ini, dua kejadian tersebut tidak saling bebas.
4. Teorema Bayes
Teorema Bayes(1720 – 1763) mengemukakan hubungan antara P (A|B) dengan P ( B|A ) dalam teorema berikut ini :
5. Kejadian saling bebas Stokhastik
(i) Misalkan A dan B adalah kejadian – kejadian pada ruang sampel S, A dan B disebut dua kejadian saling bebas stokhastik apabila kemunculan salah satu tidak dipengaruhi kemunculan yang lainnya atau : P (A | B) = P (A), sehingga:

Sebaran Peluang1. Pengertian Peubah acak dan Sebaran Peluang.
Peubah acak X adalah fungsi dari suatu sampel S ke bilangan real R. Jika X adalah peubah acak pada ruang sampel S denga X (S) merupakan himpunan berhingga, peubah acak X dinamakan peubah acak diskrit. Jika Y adalah peubah acak pada ruang sampel S dengan Y(S) merupakan interval, peubah acak Y disebut peubah acak kontinu. Jika X adalah fungsi dari sampel S ke himpunan bilangan real R, untuk setiap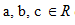 dan setiap
dan setiap  maka:
maka:

Misalkan X adalah peubah acak diskrit pada ruang sampel S, fungsi masa peluang disingkat sebaran peluang dari X adalah fungsi f dari R yang ditentukan dengan rumus berikut :

2. Sebaran Binom
Sebaran Binom atau Distribusi Binomial dinyatakan dengan rumus sebagai berikut :

Dengan P sebagai parameter dan
Rumus ini dinyatakan sebagai:
 untuk n = 0, 1, 2, …. ,n
untuk n = 0, 1, 2, …. ,n
Dengan P sebagai parameter dan
P = Peluang sukses
n = Banyak percobaan
x = Muncul sukses
n-x = Muncul gagal6. Tiga keping mata uang logam yang sama dilemparbersama-sama sebanyak 40 kali. Frekuensi harapan agarmunculnya 2 gambar di sebelah atas adalah ...A. 10B. 20C. 25D. 15JAWAB :P(dua gambar satu angka) = 1/4, makaFh = P(A) x banyak percobaan= 1/4 x 40= 10 (A)7. Dari 60 kali pelemparan sebuah dadu, maka frekuensiharapan munculnya mata dadu faktor dari 6 adalah …A. 10 kaliB. 20 kaliC. 30 kaliD. 40 kaliJAWAB :P(faktor dari 6) = = makaFh = P(A) x banyak percobaan= 2/3 x 60= 40 (D)8. Dari 900 kali percobaan lempar undi dua buah dadubersama-sama, frekuensi harapan muncul mata daduberjumlah 5 adalah …A. 300B. 225C. 180D. 100JAWAB :P(mata dadu berjumlah 5) = 4/36 = 1/9 makaFh = P(A) x banyak percobaan= 1/9 x 900= 100 (D)9. Jika sebuah dadu dilempar 36 kali, maka frekuensiharapan muncul mata dadu bilangan prima adalah …A. 6 kaliB. 12 kaliC. 18 kaliD. 24 kaliJAWAB :P(bilangan prima) = ½ makaFh = P(A) x banyak percobaan= ½ x 36= 18 (C)10 sebuah dadu di lempar sebanyak 50 kali . frekuensi harapan munculnya mata dadu genap adalah
a. 22 b. 24 c. 25 d. 26penyelesaianS = { 1 , 2 , 3 , 4 , 5 , 6 } n ( S ) = 6A = { 2 , 4 , 6 } n (A ) = 3P ( A ) =
Fn = P( A ) x n
= x 50 = 25Jadi frekuensi harapan munculnya mata dadu genap adalah 25




i appreciate your work fandi. nice, even you have copy several from others.
ReplyDelete